Variación directamente proporcional

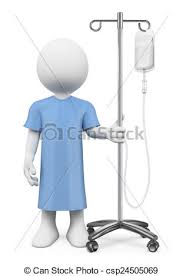
Para que dos magnitudes sean directamente proporcionales a otras dos, se debe cumplir que si una de ellas aumenta, el valor de la otra aumenta en la misma proporción a la otra o viceversa, por ejemplo si un paciente internado gasta en promedio 3 litros de suero por cada día internado, quiere decir que el número de litros de suero consumidos por el paciente es directamente proporcional a los días internado o viceversa (los días internados es directamente proporcional al número de litros de suero consumidos), a mayor número de litros consumidos, mayor será los días internado, o a mayor días internado, mayor el consumo de litros de suero.

 

3 litros           →        1 día.

6 litros           →        2 días.

18 litros           →      6 días.

    .                                  .

    .                                  .                                                                 

 Tomando en cuenta la relación anterior se deduce que si se forman razones con los valores de ambas magnitudes, la constante de proporcionalidad es siempre la misma (en este caso la razón de litros de suero a días de internado es de 3), por tanto es otra forma de ver las magnitudes directamente proporcionales.

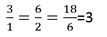
La gráfica de dos magnitudes que están en proporción directa, es un conjunto de puntos que están sobre una recta creciente que pasa por el origen del sistema de coordenadas.

Analizando el gráfico se visualiza que si una magnitud aumenta, la otra también aumenta.